Бином Ньютона — это формула, которая позволяет раскрывать степень двучлена в биномиальную сумму. Эта формула была предложена английским математиком Исааком Ньютоном и используется во многих областях науки, включая математику, физику и экономику.
Что такое бином Ньютона?
Бином Ньютона — это формула, которая позволяет раскрывать степень двучлена в биномиальную сумму. Она была разработана английским математиком Исааком Ньютоном и имеет широкое применение в различных областях науки.
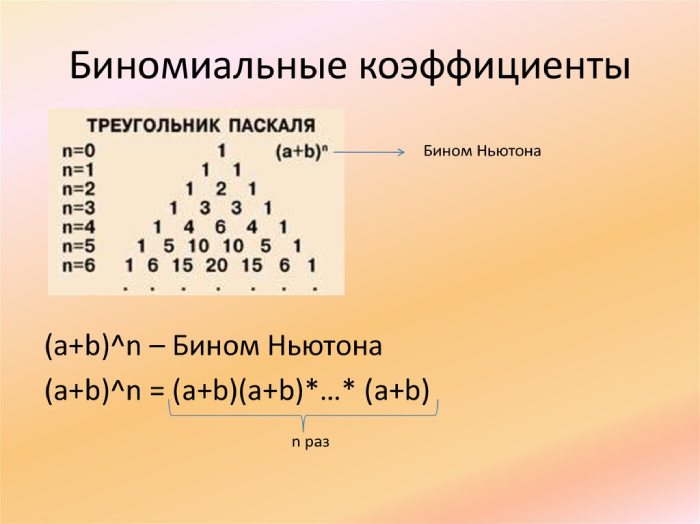
Формула бинома Ньютона имеет вид:
(a b)^n = C(n,0)a^n*b^0 C(n,1)a^(n-1)*b^1 C(n,2)a^(n-2)*b^2 … C(n,n-1)a^1*b^(n-1) C(n,n)a^0*b^n
Здесь a и b — произвольные числа (часто называемые «базой»), n — целое неотрицательное число (степень), а C(n,k)/ k=0/ /( ) = n!/ / (k!(n-k)!).
Благодаря этой формуле мы можем легко вычислять значение любой степени двучлена без необходимости многократного раскрытия скобок. Она находит применение в математике, физике, экономике и других областях.
Значение бинома Ньютона в математике
Бином Ньютона играет важную роль в математике и имеет множество приложений. Вот некоторые из них:
Разложение двучлена
Бином Ньютона позволяет разложить выражение типа (a b)^n на сумму биномиальных членов. Это полезно, когда мы хотим упростить сложные выражения или найти коэффициенты многочлена.
Коэффициенты биномиального распределения
Вероятностная статистика использует бином Ньютона для вычисления вероятности определенных событий, таких как количество успехов в серии испытаний Бернулли.
Теория вероятности и комбинаторика
Формула бинома Ньютона обеспечивает подсчет числа сочетаний или перестановок объектов без необходимости перебора всех возможных вариантов.
Решение задач физического моделирования
Благодаря объединению теории вероятности и математической физики, бином Ньютона используется для описания различных явлений в физических моделях.
Таким образом, бином Ньютона имеет широкое применение в математике и играет ключевую роль во многих областях науки и инженерии.










